Modelo M/M/2
El modelo M/M/2 es un tipo de sistema de colas que se caracteriza por tener arribos y servicios aleatorios (de tipo Markoviano) y DOS servidores. En este modelo:
- Los clientes llegan siguiendo una distribución Poisson con una tasa promedio de arribos λ (clientes por segundo).
- El tiempo de servicio sigue una distribución exponencial con una tasa promedio μ (clientes atendidos por segundo). Pero aquí la tasa se calcula haciendo la sumatoria de las tasas de servicios obtenidas con cada servidor
- Hay una sola cola y dos servidores que atienden de a un cliente a la vez.
- Las salidas son independientes de las entradas. Independientemente de la llegada de los clientes, el servidor trabaja a su velocidad
- \[ \mu_s = \mu_1 + \mu_2 \]
- \[ \rho = \frac{\lambda}{\mu_s} = \frac{\lambda}{\mu_1 + \mu_2} \]
- \[ L_s = \frac{\rho}{1-\rho} \]
- \[ L_q = \frac{\rho^2}{1-\rho} \]
- \[ w_s = \frac{L_s}{\lambda} \]
- \[ w_q = \frac{L_q}{\lambda} \]
- \[ P_0 = 1 - \rho \]
- \[ P_n = (1-\rho)\rho^n \]
Donde:
• \(\mu_s\) es la tasa de servicio total del sistema
• \(\mu_1, \mu_2\) son las tasas de servicio de cada servidor
• \(\lambda\) es la tasa de llegada de clientes
• \(\rho\) es la utilización del sistema
• \(L_s\) es la longitud promedio del sistema
• \(L_q\) es la longitud promedio de la cola
• \(w_s\) es el tiempo promedio en el sistema
• \(w_q\) es el tiempo promedio de espera en la cola
• \(P_0\) es la probabilidad de sistema vacío
• \(P_n\) es la probabilidad de tener n clientes en el sistema
Pero, desde aquí hay que saber que existen 2 tipos de sistemas M/M/2: Sistemas con Servidores a la Misma Velocidad; Sistemas con Servidores a Diferentes Velocidades.

Sistemas M/M/2 con Servidores a la Misma Velocidad
En este modelo M/M/2, los servidores no se diferencian en torno a su velocidad. Por lo tanto, sus tasas de servicio serán iguales. En este modelo la tasa de servicio total será el doble de la tasa de servicio de cada servidor.
- \[ \mu = \mu_1 = \mu_2 \]
- \[ \mu_s = 2 \cdot \mu \]
- \[ \rho = \frac{\lambda}{2 \cdot \mu} \]
Donde:
• \(\mu\) es la tasa de servicio de cada servidor individual
• \(\mu_s\) es la tasa de servicio total del sistema
• \(\lambda\) es la tasa de llegada de clientes
• \(\rho\) es la utilización del sistema
Sistemas M/M/2 con Servidores a Diferentes Velocidades
En este modelo M/M/2, las tasas de servicio provenientes de cada servidor NO son iguales, por lo tanto, tendremos que realizar las ecuaciones generales de M/M/2. Pero en ocasiones, y volviendo al tema de los sistemas M/M/1, uno de estos puede resultar insuficiente y provocar el crecimiento de las colas hacia el congestionamiento. Para diagnosticar si esto es circunstancial o permanente (donde la tasa de arribos aumenta "para siempre), se puede observar el sistema durante un periodo (por ejemplo, un mes) y aplicar el Teorema de Little para calcular N.
- \[ N = \lambda \cdot W \]
El número medio de clientes es directamente proporcional al tiempo medio de permanencia de los clientes en el sistema (W) siendo el factor de proporcionalidad la tasa de arribos.
- Si \( N < \frac{\lambda}{\mu_1 - \lambda} \), entonces el sistema está adecuado y no se modifica.
- Si \( N > \frac{\lambda}{\mu_1 - \lambda} \), entonces hay que aumentar la tasa de servicio.
- Si \( N = \frac{\lambda}{\mu_1 - \lambda} \), entonces el sistema está justo; puede convenir aumentar la tasa de servicio debido a que la tasa de arribo está aumentando.
Ante esto, se pueden aplicar 3 soluciones diferentes para el congestionamiento y arreglar un sistema insuficiente:
-
1. Cambiar el servidor por uno más rápido (Siempre funciona y mejora el rendimiento).
2. Agregar otro servidor igual o más rápido (Siempre funciona y es tanto eficaz como tolerante a fallo, pero puede ser costoso).
3. Agregar un servidor más lento (Solución de último recurso que no se recomienda, ya que su incorporación puede mejorar o empeorar el rendimiento).
Cuando tenemos que configurar un servidor más al sistema M/M/1, formando uno M/M/2, existen dos configuraciones posibles:
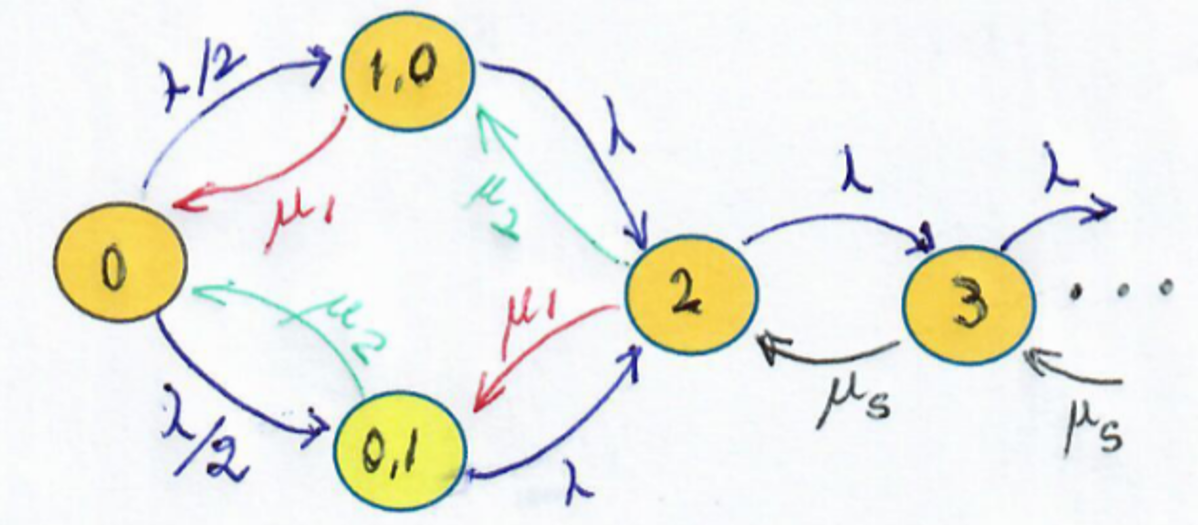
Sistemas M/M/2 Sin Selección de Servidor
Cuando ambos servidores están libres, el cliente elige al azar (misma probabilidad de ir a cualquiera de los dos servidores). A largo plazo, la mitad de los clientes irá al servidor lento, disminuyendo la velocidad de sus cálculos.
- \[ \rho_c = 1 - \left(\frac{r*(1+r)}{(1+r^2)}\right)^2, \text{ donde } r = \frac{\mu_2}{\mu_1} \]
- \[ \pi_0 = \frac{(1-\rho)}{(1-\rho+\frac{1}{a})}, \text{ donde } a = \frac{(2\mu_1*\mu_2)}{(\mu_1+\mu_2)} \]
- \[ N = \frac{\lambda}{[(1-\rho)*(\lambda+(1-\rho)*a)]} \]
Donde:
• \(\rho_c\) es el umbral crítico de utilización
• \(r\) es la relación entre las tasas de servicio (\(\mu_2/\mu_1\))
• \(\pi_0\) es la probabilidad de que el sistema esté vacío
• \(a\) es un factor que relaciona las tasas de servicio
• \(N\) es el número medio de clientes en el sistema
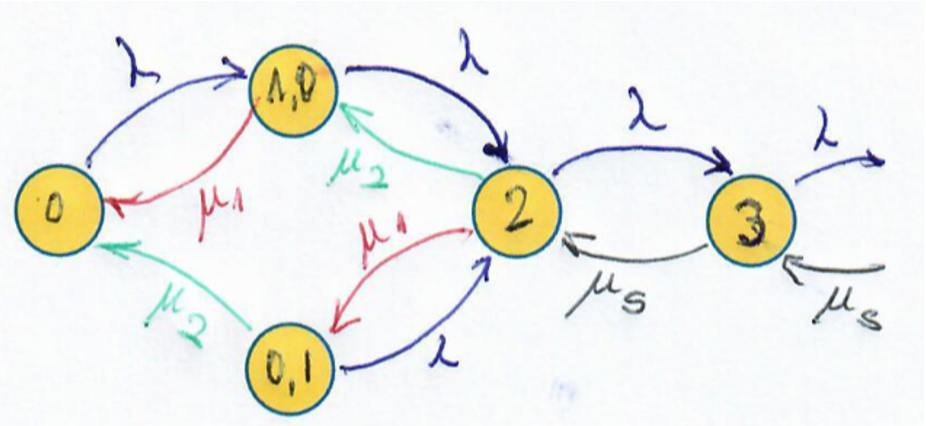
Sistemas M/M/2 Con Selección de Servidor
Si ambos servidores están libres, el cliente siempre elige el servidor rápido, mejorando el rendimiento del sistema. De alguna manera se lo direcciona, ya sea por algún algoritmo o por alguien que le indica adónde ir.
-
\[ \rho_c^2 * (1 + r^2) - \rho_c(2 + r^2) - (2r - 1) * (11 + r) = 0 \]
Se obtiene \(\rho_c\) si se resuelve la cuadrática.
- \[ \pi_0 = \frac{(1-\rho)}{(1-\rho+\frac{\lambda}{a'})}, \text{ donde } a' = \frac{(2\lambda+\mu)*(\mu_1*\mu_2)}{\mu*(\lambda+\mu_2)} \]
- \[ N = \frac{\lambda}{[(1-\rho)*(\lambda+(1-\rho)*a')]} \]
Donde:
• \(\rho_c\) es el umbral crítico de utilización
• \(r\) es la relación entre las tasas de servicio (\(\mu_2/\mu_1\))
• \(\pi_0\) es la probabilidad de que el sistema esté vacío
• \(a'\) es un factor que relaciona las tasas de servicio y llegada
• \(N\) es el número medio de clientes en el sistema